কো-অর্ডিনেট সিস্টেম ও বস্তুর অবস্থান

কো-অর্ডিনেট সিস্টেম

মনেকরো তোমার নাম কাটুশ, তুমি একজন মহাকাশচারী। স্পেসশীপে চরে একগ্রহ থেকে আরেকগ্রহে ভুস ভুস করে উড়ে বেড়াও । একদিন পৃথিবী থেকে কাজটাজ শেষ করে ব্যাগ-ট্যাগ গুছিয়ে মঙ্গলগ্রহের দিকে রওনা দিলে।

সেটা জানার জন্য প্রথমেই তোমাকে জানতে হবে কো-অর্ডিনেট সিস্টেম কাকে বলে। যেখান থেকে স্পেশশীপটা চলা শুরু করলো মনেকরো সেটা হচ্ছে কেন্দ্রবিন্দু। এবার কেন্দ্র থেকে তোমার স্পেশশীপ যেদিকে চলছে সেদিক বরাবর একটা লম্বা রেখা টানলাম। এটি হচ্ছে অক্ষরেখা। অক্ষরেখাটির নাম দিলাম x-অক্ষ।

এই অক্ষরেখায় এক কিলোমিটার পর পর দাগ কেটে কেটে ভাগ করলাম । এগুলি দিয়ে অক্ষের কেন্দ্র থেকে তোমার স্পেসশীপটা কতদূরে আছে সেটা খুব সহজেই হিসেব করতে পারবো।

এবার একক দৈর্ঘ্য বরাবর তুমি যেদিকে রওনা দিয়েছো সেদিক বরাবর ছোট ছোট ভেক্টর আঁকলাম। এই একক দৈর্ঘ্য বিশিষ্ট ভেক্টরগুলিকে বলা হয় Unit ভেক্টর।

যেহেতু আমরা ধরে নিয়েছি, তোমার স্পেসশীপটা শুধুই x-অক্ষ বরাবর ছুটছে, সেহেতু স্পেসশীপটার অবস্থান, সরণ ও গতি বোঝানোর জন্য একটি Unit ভেক্টর হলেই আপাতত চলবে। মনেকরো, x-অক্ষ বরাবর এই Unit ভেক্টরটার নাম দিলাম $\hat{i}$। যদি কেন্দ্র হতে স্পেসশীপটা সামনের দিকে যায় তাহলে সেটিকে (+ve) x-অক্ষ বরাবর এবং যদি উল্টো দিকে যায় তাহলে (-ve) x-অক্ষ বরাবর চলছে বলে ধরে নিবো।

এই একক ভেক্টর গুলির প্রত্যেকটির দৈর্ঘ্যই $|\hat{i}|=1$ এবং এরা যেহেতু একই দিকে নির্দেশ করছে, সুতরাং আমরা লিখতে পারি $\hat{i}_1=\hat{i}_2=\hat{i}_3\ldots$; একই ভাবে (-ve) x-অক্ষ বরাবর চললে এই একক ভেক্টর গুলির সামনে একটা নেগেটিভ চিহ্ন দিয়ে লিখতে পারি $-i_1=-i_2\ldots$। এই পুরো সিস্টেমটাকে এককথায় আমরা কো-অর্ডিনেট সিস্টেম বলব।

পরের অধ্যায় গুলিতে স্পেসশীপের অবস্থান, বেগ ও ত্বরণ হিসেব করার সময় এই একক ভেক্টরগুলি অনেক সাহায্য করবে।

অবস্থানের ফাংশন

এখন যেহেতু কো-অর্ডিনেট সিস্টেম আর ভেক্টর সম্পর্কে মোটামুটি ধারনা পেয়েছো, এবার আসো দেখাযাক অক্ষের কেন্দ্র থেকে মহাকাশযানটির দূরত্ব কিভাবে একক ভেক্টর ও অবস্থানের ফাংশনের মাধ্যমে প্রকাশ করা যায়।

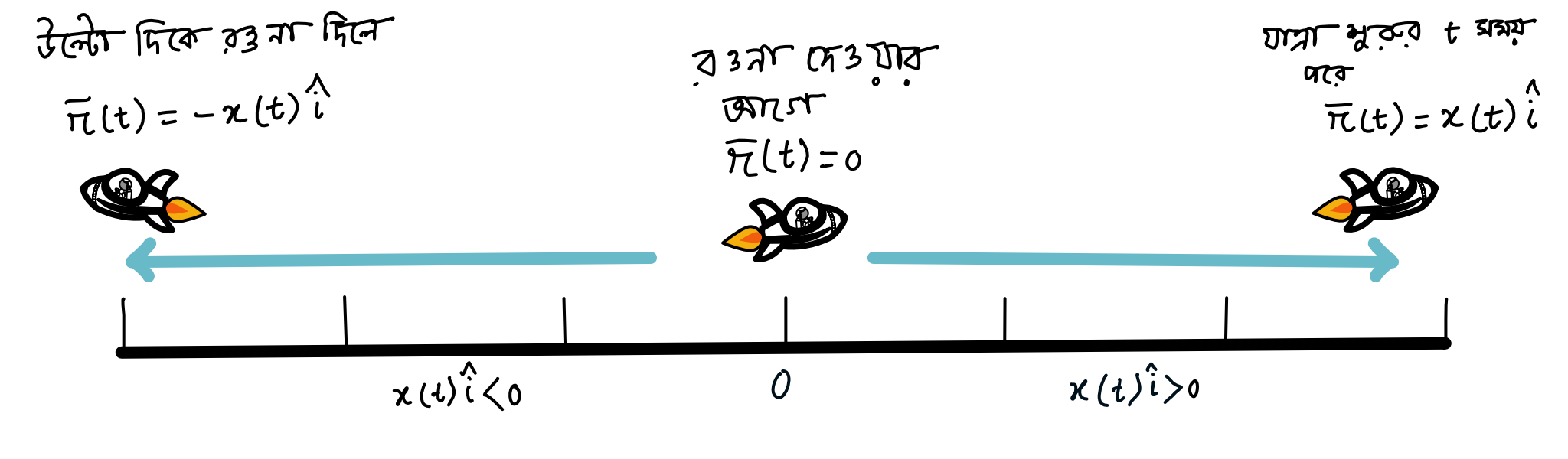
বোঝার সুবিধার জন্য মনেকরো, তুমি মহাকাশযানটি শুধুই x-অক্ষ বরাবর একটি সরল রেখা ধরে উড়াচ্ছো । এবার অক্ষরেখার কেন্দ্র থেকে তা যতটুকু দূরত্ব অতিক্রম করেছে সেই পর্যন্ত একটি ভেক্টর আকলাম। যেহেতু ভেক্টরটি মহাকাশযানটির অবস্থান নির্দেশ করছে, তাই একে বলবো অবস্থান ভেক্টর এবং এই ভেক্টরটির নাম দিলাম $\vec{r}$। মহাকাশযানটি যতক্ষন উড়বে, অক্ষের কেন্দ্র থেকে তার দূরত্ব তত বাড়তে থাকবে। সুতরাং সাথে সাথে ওই ভেক্টর $\vec{r}$ এর দৈর্ঘ্যও বাড়তে থাকবে।

ছবিঃ ২.১

যেহেতু ভেক্টরটি সময়ের সাথে সাথে বাড়ছে, এজন্য অবস্থান ভেক্টরটিকে সময়ের ফাংশন $\vec{r}(t)$ হিসাবে লিখতে পারি। একদম শুরুতে যখন তুমি মহাকাশযানটি চালানো শুরু করোনি তখন $\vec{r}(t) = 0$, এবং সময় বাড়ার সাথে সাথে মহাকাশযানটি x-অক্ষ বরাবর ধনাত্মক দিকে যেতে থাকবে, কাজেই তোমার অবস্থান ভেক্টর হবে $\vec{r}(t)=x(t)\hat{i}$। কিন্তু যদি মহাকাশযানটিকে ঘুরিয়ে উল্টো দিকে রওনা দাও, তাহলে ফাংশনটি ঋণাত্মক দিকে দূরত্ব অতিক্রম করবে অর্থাৎ অবস্থান ভেক্টরটি হবে $\vec{r}(t)=-x(t)\hat{i}$। সুতরাং আমরা তিনটি ঘটনা দেখতে পাচ্ছি, মহাকাশযানটি $x(t)\hat{i}=0$ হলে, মহাকাশযানটি আগের যায়গায় দাঁড়িয়ে আছে, $x(t)\hat{i}>0$ হলে মহাকাশযানটি $x$ অক্ষ বরাবর এগিয়ে যাচ্ছে আর $x(t)\hat{i}<0$ হলে মহাকাশযানটি দিক পরিবর্তন করে উল্টো দিকে যাচ্ছে।

লক্ষ্য করোঃ সাধারন ভেক্টরগুলির উপর $\vec{arrow}$ আর একক ভেক্টরগুলিকে মাথার উপরে একটি $\hat{hat}$-চিহ্ন দিয়ে প্রকাশ করা হচ্ছে। এভাবে x-অক্ষ বরাবর একক ভেক্টরকে নির্দেশ করবো $\hat{i}$ $\hat{i}$ এর উচ্চারণ i hat । অনেক জায়গায় একে $\hat{x}$ বা $\hat{e_i}$ দিয়েও প্রকাশ করা হয়। দিয়ে, y-অক্ষ অক্ষ বরাবর একক ভেক্টরকে নির্দেশ করবো $\hat{j}$ $\hat{j}$ এর উচ্চারণ j hat । অনেক জায়গায় একে $\hat{y}$ বা $\hat{e_j}$ দিয়েও প্রকাশ করা হয়। দিয়ে, আর z-অক্ষ বরাবর একক ভেক্টরকে নির্দেশ করবো $\hat{k}$ $\hat{k}$ এর উচ্চারণ k hat । অনেক জায়গায় একে $\hat{z}$ বা $\hat{e_k}$ দিয়েও প্রকাশ করা হয়। দিয়ে।